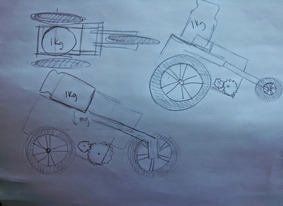
The challenge was to design a lego vehicle that is propelled by one PicoCricket motor. The vehicle must carry a 1 kg weight as fast as possible on a 4 meter straight, carpeted track.
Gear Train Practice:
Before beginning our lego car design, my partner and I worked on creating lego gear trains in order to understand the mathematics behind gear ratios/gear reductions and to get a feel for how to build with the lego pieces. The gear train pictured above has a gear reduction of 27:1. This value was found by multiplying the gear ratios together. As a class we talked about the advantages and disadvantages of different gear reductions. The higher the gear ratio, the more torque the motor and the less speed the motor has. Conversely, the lower the gear ratio is, the faster the car and the less torque the car has. Depending on the intended function of the vehicle speed or torque could be more or less important. The ultimate decision must be made with cost-benefit analysis in mind.
Design Process:
The first step in our design process was to create a gear train that would fit the needs of our race car. We built a few different gear trains and connected them to the motor. We then determined the gear ration and observed how well these gears turned. We determined from this process that a 15:1 gear reduction (pictured below) would be best for our purposes.
Once we had decided on this particular gear train we began to consider the design of the entire car. We decided that a car with a 3 wheel design would be better than a 4 wheel design because it would reduce the amount of area of the car interacting with the carpet, and reduce weight, thereby reducing friction. We also decided to construct a car that had a lateral axis that was in a wedge or angled shape. This would evenly distribute the 1 kg weight between the two wheel axles and prevent one from bearing so much weight that it would bow and not be able to turn.
Now that we had our basic deign ready, one of the biggest challenges was how to fit the wheels and motor components to the gear train without interfering with any other pieces. While building we were constantly forced to consider the order of assembly that would be most efficient, since in order to replace one piece, we often had to take apart half of the entire car.
Now it was time to test! The video below is one of our first test runs of the car. What I failed to catch on camera was that the first time that we lined the car up on the line, with the front being the single wheel, the car started moving backwards! Apparently, the motor's direction had been switched. At first we thought that it would be best to switch it back, but we found that the car actually went faster when it traveled with the two wheeled axle as the front. I think that this has a lot to do with the balance of the car. The double wheeled axle in the front allows the car to move along a straighter path, and therefore faster path, since each wheel reinforces the stability of the other. Also, the 1 kg mass is resting over top of the double wheeled axle, but because of the angle of the car it is distributed to the single wheel. This design is even better when the single wheel is in the back because it decreases the static friction present on the front wheel, that would otherwise hinder its initial motion.
Final Design:
The Race:
After the race we talked a little about the effective gear ratio versus the gear train ratio. We found that the diameter of the wheels used can greatly affect the effective gear ratio. Our wheels had a diameter of 8 cm. Since (angular velocity)(r) = Linear Velocity as the radius of the wheel increases its linear output from the angular velocity produced by the motor and gears increases as well.
We also talked briefly about the importance of considering the strength of the materials used and the friction associated with them. In the case of the car, it was important to remember that the axles are made from plastic, which will bend under significant weight. In order to ensure that our axle bent as little as possible, we moved them closer together so that the weight of the car and the 1 kg mass would not be concentrated at the ends of the axle. We also discussed friction as it related to the wheels of our car. As we suspected, the fewer wheels that are in contact with the ground, the less friction. It is also important to distinguish that wheels interact with the floor through static friction, not kinetic friction since they are rolling along the road not sliding. The coefficient of static friction for a given surface is always higher than its kinetic friction.
Reflection:
This project has helped me to grasp the concept of gear trains and the relationship between torque and speed. It also helped me to realize that there are many more things to consider when designing a real world object as compared to the simplified mathematical model. In the case of the cars, we needed to consider not only the gear ration, but the diameter of the wheels, the bend of the axle, the balance of the car, and friction between the gears themselves and between the wheels and the floor.